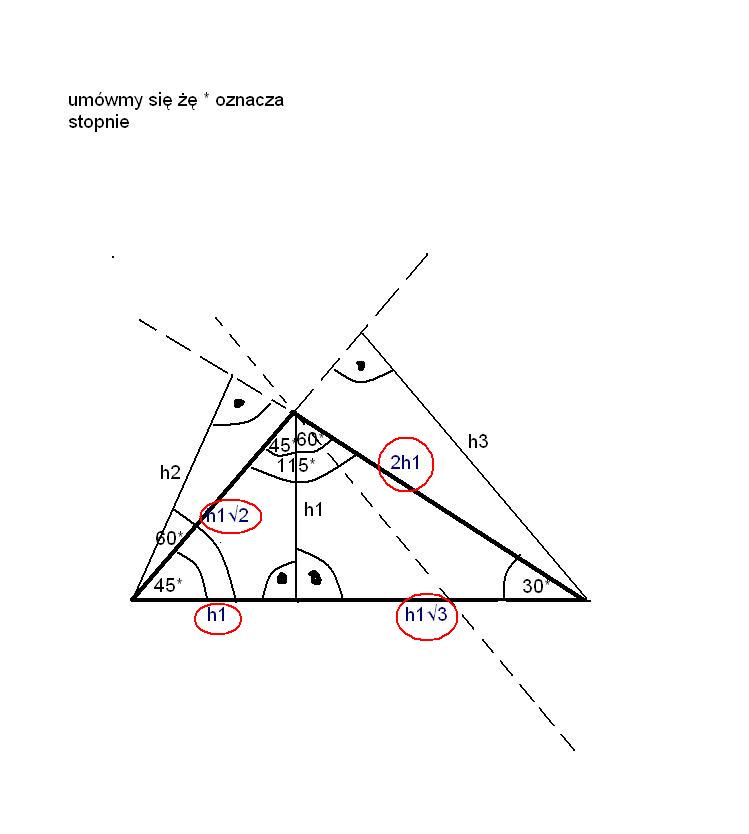
te oznaczenia na załoączniku oznaczone niebieskim kolorem( w czerwonej ramce bo niebieskiego koloru nie widze za bardzo) to wszystko wzieło sie z własności trójkątów o miarach kątów 30,6090, oraz 45,45,90, to chyba zrozumiale
więc bierzemy się do obliczen
najpierw h1:
wzór na pole trójkąta w tym pprzypadku
P=[(h1+h1√3)*h1]\2= 8+8√3
h1²+h1²√3= 16+16√3
h1²(1+√3)= 16(1+√3)
h1²=16
h1= 4 lub h1= -4(N.O.W.Z)
teraz obliczamy h2
to tez bierze się z własnosci trójkata 30, 60 i 90 stopni
h2=1/2(4+4√3)
h2= 2+2√3= 2(1+√3)
to teraz obliczamy h3
tutaj korzystamy z twierdzenia Talesa
8 do 4√2 ma sie tak samo jak 4+4√3 do h3
więc wymnażamy na krzyż
8h3= 4√2(4+4√3)
8h3= 16√2+16√6
h3= 2√2+2√3= 2(√2+√3)
to wszystko jesli coś jest dla Ciebie nie zrozumiałe to pisz na pv, na pewno wyjasnie;) lubie tego typu zadania.
a rysunek masz w załączniku
