a)V = P x H / 3
p - pole podstawy
H - wysokosc ostrosłupa
V - objętość ostosłupa
50√3 = p x 5√3 / 3 | x3
150√3 = p x 5√3 | : 5√3
p = 30cm2
a - krawedz podstawy
a² = 30
a= √30 cm
b)
między t przekątnymi ma 60 st.
sin60 =hd, skąd wyliczysz h=10√3.
Podobnie z funkcji cos60= d1d otrzymasz d1= 10cm. A d1 to przekątna kwadratu o boku
a, czyli
a√2=10.
a=5√2.
P=100+200√6, V= 500√3.
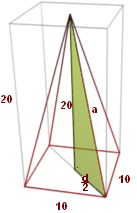
Krawędź boczną a ostrosłupa można policzyc z tw. Pitagorasa w ziolonym trójkącie prostokątnym (dolna przyprostokątna to połowa przekątnej d podstawy ostrosłupa czyli przekątnej kwadratu).tak mi się wydaje.